Examine the consistency
of the system of equations in Exercises 1 to 6.
1. x + 2y
= 2 and 2x + 3y = 3
|A|= 3- 4
|A|= -1
|A|≠ 0
Equations has unique
solutions. Hence equations are consistence
2. 2x – y = 5 and x + y = 4
|A|= 2+1
|A|= 3
|A|≠ 0
Equations has unique
solutions. Hence equations are consistence
3. x + 3y
= 5 and 2x + 6y = 8
|A|= 6-6
|A|= 0
Hence equations are inconsistence
4. x + y
+ z = 1 , 2x + 3y + 2z = 2 and ax + ay + 2az = 4
Solution
Equation third is
divided by a we get
x
+ y + z = 1
2x + 3y + 2z = 2
x
+ y + 2z = 4/a
Hence |A| ≠0
So Equations has unique
solutions. Hence equations are consistence
5. 3x–y – 2z = 2, 2y – z =-1 and –3x – 5y = 3
Multiply both matrices we get
Hence
it is inconsistence
6. 5x – y + 4z = 5,2x + 3y + 5z = 2 and 5x – 2y + 6z = –1
|A|≠0
Hence
equations are consistence


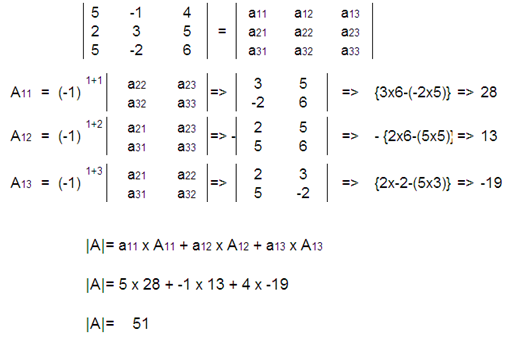
No comments:
Post a Comment